 Field lines can be used to visualize the magnetic field.
Field lines can be used to visualize the magnetic field.
Magnetic field lines have no beginning or end, they always form closed loops. (Because there are no magnetic charges, there are no sources or sinks.)
Electric charges produce electric fields.
The electric field
produced by a point charge q at rest at the origin is
E = F/q
= (keQ/r2)
(r/r).
The electric field of a charge distribution can be found using the principle of
superposition.
Field lines can be
used to visualize the electric field.
There are no magnetic charges.
Moving electric charges produce magnetic fields.
To produce a magnetic field
B, a current
density j is needed, i.e. j = ρ+<v+> + ρ-<v->
cannot be zero.
The magnetic field produced by permanent magnets is due to "magnetization
current" densities inside ferromagnetic materials. This is
atomic-scale physics, and on that scale Classical Physics fails and
Quantum Mechanics is the model that is used. Many research
groups are currently investigating the magnetic properties of various
materials, both experimentally and theoretically, and many questions
still need to be answered.
 Field lines can be used to visualize the magnetic field.
Field lines can be used to visualize the magnetic field.
Magnetic field lines have no beginning or end, they always form closed loops.
(Because there are no magnetic charges, there are no sources or sinks.)
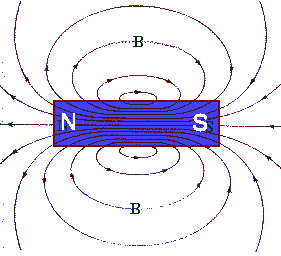
The field lines visualizing the magnetic field of a permanent bar magnet
are shown on the right.
We define the north and south pole of a bar magnet so that
inside the bar magnet the magnetic field points from the south pole (S) to the
north pole (N). Outside a bar magnet the field lines close the loop, they
exit the magnet at the north pole and enter it at the south pole.
The density of the field lines is proportional to the strength of the magnetic field.
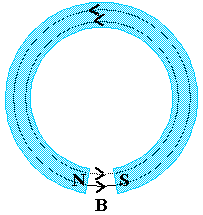 When a bar magnet is bend into the shape of a horseshoe, the magnetic
field between the poles is nearly uniform and usually quite strong.
When a bar magnet is bend into the shape of a horseshoe, the magnetic
field between the poles is nearly uniform and usually quite strong.
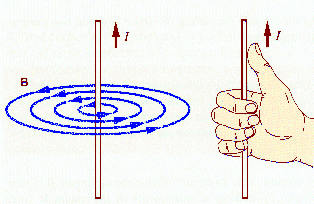 The magnetic field produced by a steady current flowing in a very long
straight wire encircles the wire. At a point P a radial distance r away
from the wire it has magnitude
The magnetic field produced by a steady current flowing in a very long
straight wire encircles the wire. At a point P a radial distance r away
from the wire it has magnitude
B = μ0I/(2πr).
This equation is derived from
one of Maxwell's equations called Ampere's law. The proportional
constant μ0 = 4π*10-7
N/A2 is called the permeability of free space.
The SI unit for the magnetic field is Ns/(Cm) = Tesla(T)
 If we imagine a circular loop of radius r, then the magnetic field is
tangential to the loop. The direction of B is given by the
right-hand rule. Let your thumb point into the direction of the current
flow. Your fingers curl into the direction of the magnetic field produced
by the current.
If we imagine a circular loop of radius r, then the magnetic field is
tangential to the loop. The direction of B is given by the
right-hand rule. Let your thumb point into the direction of the current
flow. Your fingers curl into the direction of the magnetic field produced
by the current.
The picture shows an iron-filing pattern, which reveals
the nature of the magnetic field surrounding a current-carrying wire.
A 30 A current is flowing in a long, straight wire. What is the magnetic field strength a distance 1 cm from the wire?
Solution:
The magnitude of
the field inside a
tightly wound long (compared to its radius) solenoid (away from the ends) with n = N/L
turns per unit length is
B = μ0nI.
The
direction of the field inside is given by the right-hand rule. Curl the fingers of
your right hand in the direction that the current flows in the solenoid. Your thumb points in the direction of
B. The magnetic field produced by the solenoid resembles that of a
bar magnet.
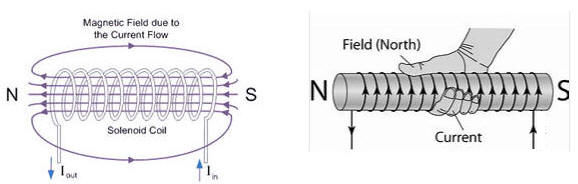
 In the picture on the right the field pattern inside a
current-carrying solenoid is revealed with iron filings.
In the picture on the right the field pattern inside a
current-carrying solenoid is revealed with iron filings.
What current is required in the windings of a long solenoid that has 1000 turns uniformly distributed over a length of 0.4 m in order to produce at the center of the solenoid a magnetic field of 10-4 T?
Solution:
For a single current loop we define the magnetic moment
μ as
μ = IAn.
(magnetic moment = current times area)
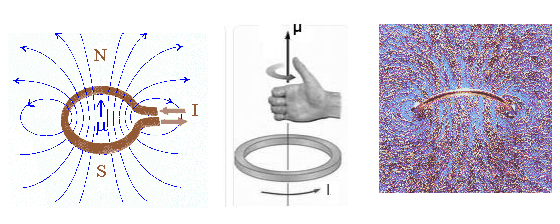
The magnetic moment (or magnetic dipole moment) is a vector. The direction of the magnetic moment is the
direction of the area vector of the loop as defined by the right-hand rule. Curl
the fingers of your right hand in the direction of the current flow. Your
thumb points into the direction of the magnetic moment μ.
The magnetic field lines of a loop with dipole moment
μ are shown on the right. The field-line pattern
is that of a small button magnet. We say that μ
points from the south pole to
the north pole of the magnet. (Magnetic field lines therefore exit
the loop at the north pole and enter at
the south pole.)
At the center of the loop the magnetic field produced by
the loop is
B = (μ0I/(2R))n,
where n is
the unit vector in the direction of the dipole moment μ.
If we have a short (compared to its radius) coil with N loops, then the magnetic
moment of the coil is
μ = NIAn,
and the magnetic field produced by
the coil at its center is is B = (μ0NI/(2R))n.
Find the magnetic field at the center of a circular loop of radius R that is formed in a long straight thin wire that carries current I. Use the SI system of units.
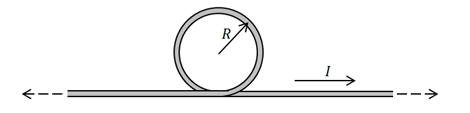
Solution:
We use a right hand rule for two different purposes.
One is to find the direction of the vector cross product. That is covered in
physics 221 which is a prerequisite for physics 222.
Review here:
Vector Product
The other purpose is to relate the direction of a current to the direction of the magnetic field or the magnetic moment it produces. There are two cases where this works.
(a) We have current flowing in a straight wire and the magnetic field lines
form circles around the wire.
(b) We have current flowing in a wire forming a loop or a coil, and the
magnetic field in the middle of the loop or coil is perpendicular to the loop
and straight inside the coil.
In other words, we have something that is straight, and something that curls.
Then if the thumb of your right hand points in the direction of the thing that
is straight, then the fingers of you right hand curl in the same direction of
the thing that is curling, and vice versa.